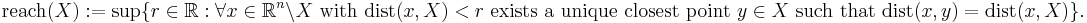Reach (mathematics)
In mathematics, the reach of a subset of Euclidean space Rn is a real number that roughly describes how curved the boundary of the set is.
Definition
Let X be a subset of Rn. Then reach of X is defined as
Examples
Shapes that have reach infinity:
- single point
- straight line
- full square
- any convex set
The graph of ƒ(x) = |x| has reach zero.
A circle of radius r has reach r.
References
- Federer, Herbert (1969), Geometric measure theory, series Die Grundlehren der mathematischen Wissenschaften, Band 153, New York: Springer-Verlag New York Inc., pp. xiv+676, ISBN 978-3540606567, MR0257325